散列树形搜索反碰撞算法的研究

引言

无线射频识别技术(Radio Frequency Identification, RF ID)是利用射频信号和空间耦合(电感或电磁耦合)传输特性自动识别目标物体的技术 。RF ID系统一般由电子标签(应答器, Tag)和阅读器(读头, Reader)组成。阅读器负责发送广播并接收标签的标识信息;标签收到广播命令后将自身标识信息发送给阅读器。当阅读器识别区域内存在两个或者两个以上的标签在同一时刻向阅读器发送标识信息时,将产生冲突,解决冲突的方法称为反碰撞算法。

对于反碰撞问题, EPCglobal组织提出了基于位的二叉树算法和基于ALOHA的算法, ISO组织制定了自适应协议和二叉树搜索算法 , ISO 的自适应协议和EPCglobal的基于ALOHA的算法非常相似。诸多学者对反碰撞问题做了深入探讨:文献[ 2, 9 ]通过调整最大阅读时间间隔来降低因碰撞引起的错误拒绝问题,未阐述具体反碰撞措施;文献[ 4, 5 ]的机理是基于位的二叉树算法,算法的实施需要阅读器检测数据碰撞比特位的准确位置;文献[ 10, 11 ]分别提出了不同的标签数目估计算法( TEM) ;文献[ 12 ]运用自适应环协议解决碰撞问题,与文献[ 11 ]有异曲同工之效,但文献[ 11, 12 ]的反碰撞算法对于标签数目巨大,帧长度受限的情况无能为力;文献[ 13 ]提出了改进的动态帧时隙ALOHA 算法EDFSA(Enhanced Dynamic Framed Slotted ALOHA)反碰撞算法,通过将标签分组来限制响应标签数目,保证标签识别效率期望值在34. 6% ～36. 8%之间。本文提出散列树形搜索反碰撞算法,该算法无需阅读器检测数据碰撞比特位的准确位置,标签识别效率期望值突破了EDFSA算法36. 8%的界限,在识别大量标签时,标签识别时间小于EDFSA算法所需时间。

1　动态帧时隙ALOHA算法

动态帧时隙ALOHA (Dynamic Framed Slotted ALOHA,DFSA)算法,将时间划分成时间片(称为时隙) ,阅读器命令以及标签的数据发送必须在给定时隙内完成。阅读器发送命令后,等待一组时隙,接收来自标签的数据信息。这组时隙构成一帧,时隙的个数称为帧长度。标签收到阅读器命令后,在帧长度范围内,随机选择时隙发送数据,这样就出现了唯一时隙(只有一个标签选择的时隙) 、碰撞时隙和空时隙。为减少标签碰撞,根据标签数目确定合适的帧长度是非常重要的。动态改变帧长度有两种简单方法 ,即门限值法和指数法。但它们对标签数目的估计比较粗略,算法灵敏度低。

改进的动态帧时隙ALOHA算法EDFSA有较好的标签数目估计算法。若用三元组< c0 c1 ck >表示一帧中空时隙数、唯一时隙数和碰撞时隙数, L表示帧长度(下文中使用此符号将不再说明) ,目前EDFSA算法常采用下面三种估计标签数的方法:

1) 用公式2ck + c1 +ξ估计(ξ表示修正值);
2) 用碰撞比例ck /L 估计 ;
3) 用2. 3922ck 估计。

EDFSA算法能根据标签数估计值动态改变帧长度,当标签数目超过系统允许的最大帧长度时,采用分组策略,限制响应标签数目, 保证标签识别效率期望值稳定在34. 6% ～3618%之间。但是EDFSA算法的标签识别效率期望值没有突破36. 8%的界限。为此,本文提出散列树形搜索反碰撞算法,其标签识别效率期望值保持在36. 8%～1之间。

2　散列树形搜索反碰撞算法

标签通过散列运算选择时隙,若散列溢出会造成多标签在同一时隙中碰撞,阅读器选择碰撞时隙的标签进行递归搜索识别,直观上标签识别轨迹呈n叉树状,为此,本文称这种解决标签冲突的方法为散列树形搜索反碰撞算法。

2. 1　算法遵循的原则
1) 时隙分配原则
散列树形搜索反碰撞算法标签通过散列运算选择帧时隙,而不是随机选择时隙。散列运算用于建立从标签关键码到帧时隙的映射,这一过程由散列函数完成。一般情况下,散列函数是一个压缩映射函数。考虑到算法的实用性,本文选用式(1)所示的散列函数作为标签时隙分配原则。

hash ( key) = (õkey /w」) %L (1)

其中, key表示标签的关键码, w 为阅读器发送给标签的正整数,为保证散列的效果,帧长度L一般取质数。例如,若某标签的关键码key为12345,阅读器发送给标签的w、L值分别为59、19, 根据式(1) 得Hash ( key) 等于0, 那么关键码为12345的标签选择第0时隙发送数据。

2) 帧长度改变原则
动态改变帧长度是保证反碰撞算法标签识别效率的典型措施,散列树形搜索反碰撞算法根据碰撞率和搜索深度动态改变帧长度。改变原则是:当2. 3922ck大于当前帧长度且不大于系统允许的最大帧长度时, 下一帧的帧长度改变为与当前帧长度的2倍最邻近的质数,此时,下一帧称为当前帧的扩展帧,当前帧是下一帧的原始帧;否则, 选择当前帧中一碰撞时隙,选取不大于当前帧长度的质数作为帧长度开始深度搜索,此时当前帧称为下一帧的父帧, 下一帧称为当前帧的子帧。

3) 散列参数选择原则
散列溢出会造成标签碰撞。例如,阅读器识别域内有两个标签关键码分别为key1 = 54321, key2 = 54380,当w = 1, L =59时,由式(1) 得, hash ( key1) = hash ( key2) = 41,即两标签同时在第41时隙发送数据,碰撞由此产生。散列树形搜索反碰撞算法通过递归搜索碰撞时隙, 识别出发生碰撞的所有标签。递归搜索时, 必须适当改变散列参数,使父帧映射到同一时隙的标签尽可能映射到子帧的不同时隙。分析碰撞标签关键码的特点,会发现上面例子中两个标签的关键码可分别表示为: key1 = 54321 = 920 ×59 + 41, key2 =54380 = 921 ×59 + 41。

显然, key1、key2最大差异在于它们包含不同个数的59, 所以, 要将两个标签分配到不同时隙,只需在子帧中令w = 59, L = 19, 进行散列运算, 即得
hash ( key1) = 8, hash ( key2) = 9,这样在子帧中,两标签会在不同时隙发送数据,避免了再次冲突。

由此启示得出散列运算参数w 的改变原则是:子帧的w值是父帧w与L的乘积。另外,值得说明的是,运用式(1) 所示的散列函数进行递归搜索时,能够区分出所有碰撞标签,即能保证递归返回。这是因为算法的极限情况为w、L 都等于2,此时相当于比较两个关键码的每一位, 不相等的两个数至少有一位不等,故散列深度搜索可以识别出所有标签。

2. 2　算法描述
(1) 阅读器和标签交互过程
阅读器向标签发送命令字,标签根据命令字,决定是否响应及在何时隙响应阅读器命令。阅读器收到标签响应后,向标签发送确认,标签收到确认后,进入休眠状态,称为已读标签。

(2) 重要数据结构
标签自身变量: ftag 和stag 分别表示帧号和时隙号, 用于匹配阅读器命令的相应域,决定是否响应阅读器命令。初始状态为ftag = stag = - 1。阅读器命令字Comm and (w, L, f, s) :其中f、s用作标签选择,分别表示帧号、时隙号。若s等于- 1, 选取新进入阅读器识别区域的标签和ftag 等于f的所有未读标签响应。s大于- 1时, 仅选取于ftag等于f且stag等于s的未读标签。w、L用作被选标签散列运算的参数,确定响应时隙。

二维表Table[N um W FL en S qu Flag ]:阅读器用该表以帧为单位记录标签识别轨迹。其中, N um 列表示帧号,W 列表示该帧标签散列运算时的w值, FL en列表示帧长度, S qu列是该帧的碰撞时隙队列, Flag列标识该帧是否为下一帧的原始帧(1:是, 0:非) 。

(3)算法描述
散列树形搜索是应用于RF ID系统的反碰撞算法,算法的实施依赖于阅读器和标签。因此下面分两部分描述算法的详细流程。表1给出了算法描述中所用符号的含义。

阅读器算法流程如下:
步骤1: L = 59, w = 1, f = 0, s = - 1;
步骤2: Comm and (w, L, f, s) ; squ = Generate_queue ( ) ;Add_recorder( f, w, L, squ, 0) ;
步骤3: if ( ! ck ) { delete ( f) ; f - - ; goto步骤7; } else goto步骤4;
步骤4: if (2. 3922ck > = L ) goto步骤5; else goto 步骤6;
步骤5: if ( prim e (23 L) > LMAX ) goto 步骤6;
else {L = prim e (23 L) ; s = - 1; w = 1; SetFlag ( f) ; f ++;Comm and (w, L, f, s) ; squ = Genera te_queue ( ) ;A dd_recorder( f, w, L, squ, 0) ;} goto 步骤3;
步骤6:
if (L en ( f) > 5) L = 5; else L = L ittle (Len ( f) ) ;
s = S lot ( f) ; w = Len ( f) 3 W eigh t ( f) ; f ++;
Comm and (w, L, f, s) ; squ = Generate_queue ( ) ;
Add_recorder( f, w, L, squ, 0) ;goto步骤3;
步骤7: if ( Flag ( f) ) { delete ( f) ; f - - ; goto 步骤9; } else goto 步骤8;
步骤8: deleteS lot ( f) ; if ( S lot ( f) = = - 1) { delete ( f) ; f - - ; goto步骤9; } else goto 步骤6;
步骤9: if ( f < 0) 算法结束; else goto步骤7;

标签算法流程如下:
步骤1: ftag = stag = - 1;
步骤2:接收命令(w, L, f, s) ;
步骤3: if ( s = = - 1) { 根据式(1) 计算stag; 在第stag时隙发送数据; }else { if ( f = =ftag ) {根据式(1) 计算stag; 在第stag时隙发送数据; } }
步骤4: if (收到阅读器确认) {不再响应同一阅读器的请求; 算法结束; }else { ftag ++; goto步骤2; }

3　算法性能分析与比较

3. 1　算法复杂度分析
散列树形搜索反碰撞算法运用散列运算将标签分组,减少碰撞,通过递归深度搜索识别碰撞标签。如用T ( n表示识别n个标签的时间复杂度, i表示分组数, j表示每组的标签个数,则可列出时间复杂度的递归方程,如公式(2) 所示:



本算法的最坏情况是:递归深度搜索标签时, 碰撞频繁,导致帧长度L为2, w为2的x次幂,也即该算法的特例———二叉树搜索反碰撞算法。此时i = j = 2, 由(3) 得, T ( n) =O ( n) 。

算法的空间复杂度取决于搜索深度, 最坏情况仍然是二叉树状搜索,搜索深度约为log2 n + 1。所以, 散列树形搜索反碰撞算法的空间复杂度S ( n) = O ( log2 n) 。

3. 2　识别效率分析比较
本节采用文献[ 13 ]的算法性能评价标准,定义标签识别效率,如表达式(4) 所示。一般认为在唯一时隙可以正确识别标签,因此唯一时隙数在帧中的比例能够体现系统的时隙有效利用率,用其作为标签识别效率的衡量标准是合理的。

α =c1/L×100%                    (4)
下面用n表示出现在阅读器识别域内的实际标签数目, m表示整个标签关键码空间, pk 表示同一时隙被k个标签占有的概率, ak 表示被k个标签占有的时隙数的期望值。在概率论中可以用a1 估计c1 ,于是系统效率期望值η可用(5) 表示。

η = E (α) =a1/L×100%                   (5)

EDFSA算法运用帧长度L和标签数n趋于相等时,系统有最大识别效率36. 8% 这一原理[13 ] , 通过估计标签数目来确定帧长度,使得帧长度和标签数趋于相等,当估计标签数超过最大帧长度时, 以分组的方式, 限制响应标签数, 保证帧长度与响应标签数趋于相等,使标签识别效率稳定在34. 6% ～36. 8% 之间。

散列树形搜索反碰撞算法, 运用散列方法将标签映射到帧时隙内,第一帧w为1,相当于将标签关键码空间分为L组,每组有m /L个标签(最后一组可能少一些) 。k个标签占有同一时隙的情况是由于m /L个标签中有k个标签随机出现在阅读器识别区域内而产生的, 因此, 散列树形搜索反碰撞算法中,第一帧pk 表达式为式(6) 。当然, 如散列树形搜索反碰撞算法所描述的那样,以后的各帧关键码空间将不断缩小,其效率问题可从讨论第一帧效率函数特性而得到。



下面讨论散列树形搜索反碰撞算法第一帧的单调性、极值问题,式(7) 求导得:



式(9) 说明η是r的单调递增函数;式(10) 则表明,当r趋近于0时,η有最小极限值36. 8%。也就是说, 当帧长度远小于标签关键码空间时, 识别效率期望值为36. 8% , 随着帧长度与标签关键码空间的比例增大,识别效率随之增加。下面论证空时隙概率与r的关系。

由(6) 式得: p0 = (1 - L /m ) m /L = (1 - r) 1 / r。

p0 单调性和极值证明:




所以, p0 是r的单调递减函数,当r趋近于0时, p0 趋近于0. 368。也就是说,当帧长度远小于标签关键码空间时,空时隙有最大概率0. 368,随着帧长度与标签关键码空间的比例增大,空时隙概率下降。

假设第二帧是对碰撞时隙的深度搜索, 不是第一帧的扩展帧,那么按照算法流程,第二帧的w值应等于第一帧的帧长度L,帧长度设为L ′,于是pk ,η表达式如(11) (12) :



显然LL ′/m>L/m, 前面已经证明所以η是r的单调递增函数,所以第二周期的识别效率要高于第一周期的识别效率。同理,如算法流程中描述的那样, 随着帧号的增大, 标签识别效率期望值逐步提高。

3. 3　识别时间仿真比较
根据EDFSA算法和散列树形搜索反碰撞算法的基本思想,编写了仿真程序。在仿真环境下, EDFSA初始帧长度为10,两算法最大帧长度为256时,系统识别总时间随着标签数目的变化情况如图1所示。当标签数目小于60时, EDFSA算法总体识别时间小于散列树形搜索反碰撞算法的总体识别时间,这是因为散列树形搜索反碰撞算法初始帧长度为59,标签数小于59时,可能浪费时隙。当标签数目大于60时,两种算法的系统总体识别时间与标签数目呈线性关系。这说明两种算法在标签数目大于最大帧长度时,都有分组标签的作用,限制了响应标签数,使识别时间与标签数目保持线性关系。但两条曲线的斜率不同,在标签数目较多时,散列树形搜索反碰撞算法优于EDFSA算法,这是因为散列树形搜索反碰撞算法有较高的识别效率。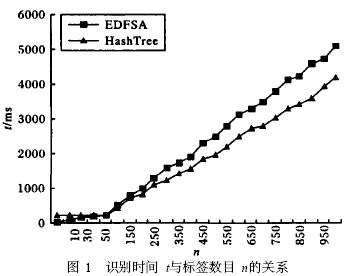



图1　识别时间t与标签数目n的关系

4　结语

本文在分析DFSA、EDFSA等目前流行的RF ID系统反碰撞算法优劣的基础上,针对EDFSA算法识别效率期望值不能突破36. 8%、基于位的二叉树搜索算法要求阅读器检测碰撞数据比特位的准确位置等不足,提出了散列树形搜索反碰撞算法。该算法运用散列运算为标签分配时隙,通过树形深度搜索解决碰撞,提高了标签识别效率。文中阐述了算法遵循的三原则,设计了算法的详细流程。通过建立并分析标签识别效率的评价模型,证明了散列树形搜索反碰撞算法标签识别效率期望值在36. 8%～1之间,优于EDFSA算法34. 6%～36. 8%的系统识别效率期望值。仿真验证表明,当标签数目大于60时,该算法的标签识别总时间比EDFSA算法的少,特别是在标签数目很大时,该算法表现出明显优势。另外,散列树形搜索反碰撞算法不需要阅读器检测碰撞数据比特位的准确位置,简化了RF ID系统的软件设计。散列树形搜索反碰撞算法突破了传统ALOHA反碰撞算法标签识别效率期望值36. 8%的界限,在标签数目很大的场合,算法性能表现良好。该算法对解决反碰撞问题有理论意义,也势必推动RF ID系统在矿山跟踪系统、汽车监控、电子支付等领域的应用。